Rheology
某一种特定材料的应力与应变关系称为该材料的应力-应变曲线(stress-strain curve)。每一种材料都有唯一的应力-应变曲线,该曲线可以通过记录材料在不同的拉伸和压缩加载(应力)下的形变(应变)来获得。这条曲线也提供了很多该材料的特性,例如其弹性模量、降伏强度(弹力限)、极限拉伸强度,也可以看出材料是脆性材料还是延展性材料。
一般而言,有关任何变形下,应力和应变的关系都可以视为是应力-应变曲线。应力和应变可以是正应力及正应变,剪应力及剪应变,也可以是混合的。可以是单一轴向、双轴或是多轴的,甚至可以是时变的。变形可以是压缩、拉伸、扭转、转动等。若没有特别标明,应力-应变曲线是指在拉伸测试下正向应力及正向应变之间的关系。
1. 拉伸¶
单轴拉伸是材料力学中常见的实验方式,用于研究材料的应力应变行为。在单轴拉伸实验中,材料在一个方向上受到拉伸力,通常与这个方向平行,而在其他方向上则受到较小的或零力。圆柱试样在拉伸时候的应力-应变曲线。我们定义工程应力为$\sigma_e = \frac{F}{A}$,工程应变为$\epsilon_e = \frac{L-L_0}{L_0}$。其中,$A$是拉伸前式样的横截面积,$L_0$是拉伸前长度。但是,随着拉伸会出现颈缩的现象,这时由于横截面积减小,计算出的工程应力就会相应增大。所以说,工程应力是为了测试的简便而采取的估计。
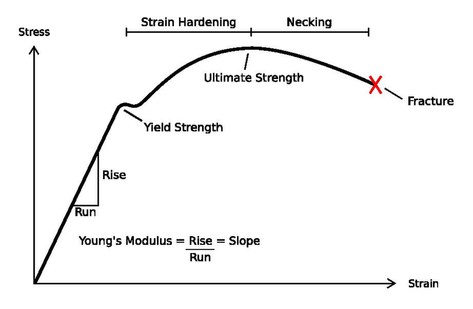
右图是室温下低碳钢的应力-应变曲线,曲线的不同阶段有不同的特性,也有不同的机械性质。而其他材料也可能会省略其中的一些阶段,或是出现其他的阶段。
第一阶段是线性弹性阶段。此阶段的应力和应变成正比,遵守胡克定律,其斜率即为杨氏模量。材料在这个阶段的变形都是弹性变形,此阶段的结束是塑性变形的开始,该点的应力即为降伏强度(或是上降伏点,简称UYP)。
第二阶段是应变硬化阶段。其应力超过降伏强度,小于极限强度(ultimate strength point)。极限强度是应力-应变曲线的最高点。这个区域一开始的应力不随应变变化,有短暂的水平区,之后,其应力随著材料伸长而变大。平坦区的应力称为下降伏点(LYP),是因为赖得带的形成及传递所造成。明显的,非均质塑性变形会在上降伏强度形成赖得带,将变形扩散到下降伏强度的材料。当材料再度均匀变形时,随著材料的伸展,其应力会增加,这称为加工硬化。因为塑性变形引起的致密位错使位错无法再进一步发展。为了要克服这种阻碍,需要加较大的临界分解剪应力。在应变累积时,材料也就在进行加工硬化,一直到应力到达极限强度为止。
第三阶段是颈缩阶段,应力超过极限强度后,试料中会出现颈缩(Necking)现象,也就是某一段的截面积明显比平均截面积要小。颈缩变形是非均质的,因为应力在截面积较小的区域更容易集中,因此颈缩会自我增强,让应力更集中。这种正回授会让颈缩很快就生成,并且很快断裂。不过此时拉力虽在减少,但其加工硬化仍在进行中。此时用真实截面积计算的真应力会继续增加,但假设截面积不变的工程应力就会减少。第三阶段的最后是材料的断裂。在断裂后可以计算材料的伸长量以及截面积的缩减量。
真实应力和应变的关系会考虑到截面积缩小对应力的影响,以及因应变参考长度使用当时长度(而不是原始长度)造成的应变降低,和工程应力及应变之间的关系有些不同。我们定义真实应力$\sigma_t = \frac{F}{A_i}$,其中$A_i$指的是颈缩区域的真实截面积(cross-sectional area)。真实应变则可以通过体积不变导出$\sigma = \int{\delta L / L} = \ln{L/L_0} = ln(1+epsilon_e)$。真实应力应变与工程应力应变之间的关系是:

$$ \sigma_t = \sigma_e(1+\epsilon_e) \epsilon = ln(1+\epsilon_e) $$
如果要全面描述应力,需要引入应力张量的概念。将应力分解为三个正交独立的分力$\sigma_1, \sigma_2, \sigma_3$。
分力的方向通常和坐标轴方向$n_1, n_2, n_3$不重合,得到:
$$ \begin{array}{c} t_{1}=T_{11}n_{1}+T_{12}n_{2}+T_{11}n_{3}\\ t_{2}=T_{21}n_{1}+T_{22}n_{2}+T_{23}n_{3}\\ t_{3}=T_{31}n_{1}+T_{32}n_{2}+T_{33}n_{3} \end{array} $$
写成张量形式有:
$$ {\left[\begin{array}{l}{t_{1}}\\ {t_{2}}\\ {t_{3}} \end{array}\right]}={\left[\begin{array}{l}{T_{11}\,T_{12}\,T_{13}}\\ {T_{21}\,T_{22}\,T_{23}}\\ {T_{31}\,T_{32}\,T_{33}}\end{array}\right]}{\left[\begin{array}{l}{n_{1}}\\ {n_{2}}\\ {n_{3}}\end{array}\right]} $$
如果沿x轴单轴拉伸,应力张量可以写作
$$ \sigma = \left[\begin{array}{ll} \sigma_{xx}& 0& 0\\ 0& 0& 0\\ 0& 0& 0 \end{array} \right] $$
根据力的性质不同,应力张量可以分解表示。各向同性压力的体系中,常将应力张量分解为:
$$ \mathbf{T} = \frac{1}{3}(\text{tr}\mathbf{T})\mathbf{I} + \mathbf{\sigma} $$ 其中$\text{tr}\mathbf{T}$是张量的迹,$\mathbf{I}$是单位张量,$\mathbf{\sigma}$是偏应力张量。偏应力张量也是对称张量,只有六个独立分量,三个为法向分量$\sigma_{ii}$,三个为剪切应力分量$\sigma_{ij} = \sigma_{ji}$
定义: $ -p = \frac{1}{3}(\text{tr}\mathbf{T}) $
则有: $ \mathbf{T} = -p\mathbf{I} + \mathbf{\sigma} $
或者写成分量式: $ \mathbf{T}_{ij} = -p\delta_{ij} + \sigma_{ij} $ $p$则为各向同性压力,例如静水压力。他作用在曲面法向上,且沿曲面任何法向的值相等,符号则是表示压力方向指向封闭曲面内部。$\delta_{ij}$是Kronecker记号,是单位张量的等价表示。
2. 剪切¶
剪切应力(通常用$\tau$表示)是与材料截面共面的应力分量。它来源于剪切力,即力矢量与材料截面平行的分量。而正应力则来源于垂直于材料截面的力矢量分量。如下图所示,可以得到剪切应力与剪切应变的关系:
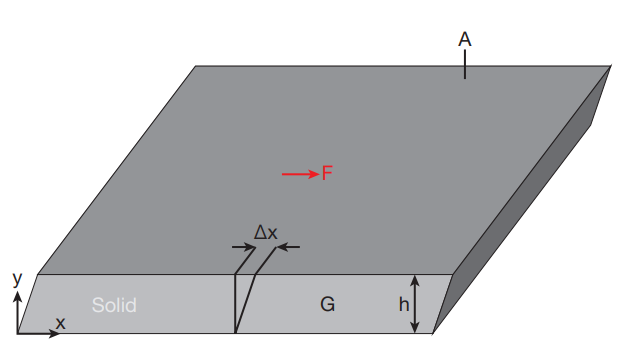
$$F/A = G \frac{\Delta x}{h}$$
$$\tau_{xy} = \frac{F}{A} = G\gamma_{xy}$$
其中,$G$是剪切模量,$\gamma_{xy}$是剪切应变。类比于弹性系数,剪切模量是材料的一种弹性模量,用于描述材料在剪切应力作用下的应变能力。剪切模量是材料的刚度,是材料的弹性模量中的一种。剪切模量越大,材料的刚度越大,材料的弹性越好。剪切模量的单位是帕斯卡(Pa)。
均匀剪切力也可以通过张量形式给出。例如,沿x轴方向的剪切力可以写作:
$$ \mathbf{T} = \left[\begin{array}{ll} 0& \tau_{xy}& 0\\ \tau_{yx}& 0& 0\\ 0& 0& 0 \end{array} \right] $$
3. 粘弹性¶
艾萨克·牛顿爵士是第一个提出描述流体阻力假说的人。1686年,他在《自然哲学的数学原理》一书中的名为"论液体的圆周运动"的章节中发表了这项工作。他的假说明确阐述了我们今天所知的牛顿流体的特性: "即流体部分缺乏流动性所产生的阻力,其他条件相等,与液体各部分相互分离的速度成正比。" 牛顿将这种现象描述为"defectu lubricitatis",即两个流体粒子之间的"缺乏润滑性",并将其归因于"attritus",即内部摩擦或粘性摩擦。从那时起,"内部摩擦"和"粘性摩擦"这两个术语一直可以互换使用。尽管牛顿的原始论文中有一个错误,150年后由乔治·斯托克斯爵士纠正,但他的主要结论仍然正确。
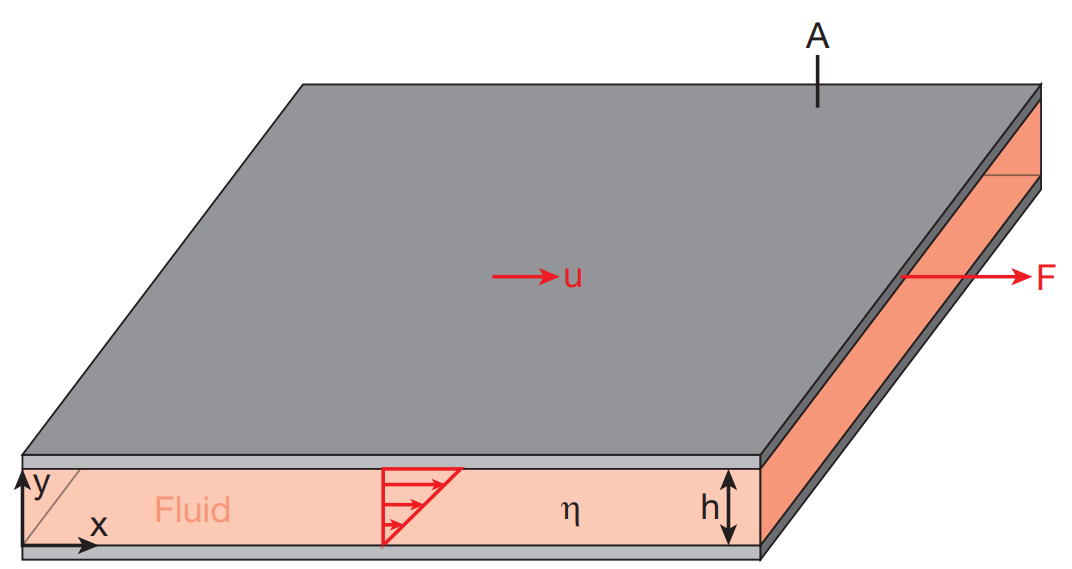
分析平行板之间的粘性流体,我们有:
$$ F / A = \eta \frac{u}{h} \tau_{xy} = \eta \frac{du}{dy} $$ 其中,$\eta$是粘度,$u$是速度,$h$是平板间距,$y$是距离平板的距离。粘度是粘性流体的一种物理性质,是流体抵抗流动的特性。粘度越大,流体的黏性越大,流动越困难。粘度的单位是帕斯卡秒(Pa·s)。
弹性的概念则是由牛顿的头号敌人罗伯特·胡克提出。当胡克声称牛顿关于引力的工作是基于他所做的工作时,两人之间产生了敌意。因此,爵爷的执念就是把胡克挫骨扬灰。在胡克1703年去世两年后,牛顿成为了皇家学会的主席,并抹去了皇家学会对胡克的一切记忆。肖像和实验室设备等在皇家学会1705年迁至新址后都神秘地消失了。
胡克是第一个发现线性弹性固体中力与挠度关系的人,并在1678年的《Lectures de Potentia Restitutiva》或《Of Spring》一书中发表了这项工作。我们今天所称之为胡克弹簧,用胡克的话来概括就是“Ut tension sic vis”或“As the extension, so the force。”简单来说,力$F$与挠度$\Delta x$成正比。
胡克的概念在1727年被莱昂哈德·欧拉修改,他用应力$F/A$表示力,用应变$\Delta/h$表示位移,其中$h$表示原始长度,$G$为弹性模量或刚度,由此得到了第2节中的定义:
$$F/A = G \frac{\Delta x}{h}$$
$$\tau_{xy} = \frac{F}{A} = G\gamma_{xy}$$
在牛顿和胡克提出他们的流体和固体模型之后,世界还需要等待近两个世纪,才有人尝试对在变形过程中具有粘性和弹性力组分的物体进行建模。1867年,詹姆斯·克拉克·麦克斯韦发表了他的论文《关于气体的动力学理论》,其中他提出了一个结合弹性和粘性效应的系统模型。他的模型以及由此产生的关于应力和应变的线性微分方程,代表了今天的麦克斯韦模型。
我们将一个粘弹性材料的应力和应变分解为弹性和粘性部分。弹性部分我们可以用胡克弹簧表示,而粘性部分则由黏壶模型表示。麦克斯韦模型是由黏壶和弹簧串联得到的线性的粘弹性模型。其中粘性和弹性效应是独立的,形变时黏壶不受弹簧约束,可产生大形变。麦克斯韦模型可用于描述液体流动性质。
$$ \tau_{xy} = \tau^{G}_{xy} = \tau^{\eta}_{xy} \\ \gamma_{xy} = \gamma^{G}_{xy} + \gamma^{\eta}_{xy} = \frac{1}{G}\dot{\sigma} + \frac{1}{\eta}\sigma $$ 由上式得: $$ \sigma + \lambda_1\dot{\sigma} = \eta_0\dot{\gamma} $$ 其中,$\lambda_1 = \eta_0 / G$被称为松弛时间,单位为秒。$\dot$ 是指对时间的一阶偏微商。
%load_ext lammpscn.lammps
LAMMPS (3 Aug 2023 - Development - patch_2Aug2023-747-ge655cda066) OMP_NUM_THREADS environment is not set. Defaulting to 1 thread. (src/comm.cpp:98) using 1 OpenMP thread(s) per MPI task
%%cmd
# Sample LAMMPS input script for viscosity of liquid Ar
units real
variable T equal 200.0 # run temperature
variable Tinit equal 250.0 # equilibration temperature
variable V equal vol
variable dt equal 4.0
variable p equal 400 # correlation length
variable s equal 5 # sample interval
variable d equal $p*$s # dump interval
# convert from LAMMPS real units to SI
variable kB equal 1.3806504e-23 # [J/K] Boltzmann
variable atm2Pa equal 101325.0
variable A2m equal 1.0e-10
variable fs2s equal 1.0e-15
variable convert equal ${atm2Pa}*${atm2Pa}*${fs2s}*${A2m}*${A2m}*${A2m}
# setup problem
dimension 3
boundary p p p
lattice fcc 5.376 orient x 1 0 0 orient y 0 1 0 orient z 0 0 1
region box block 0 4 0 4 0 4
create_box 1 box
create_atoms 1 box
mass 1 39.948
pair_style lj/cut 13.0
pair_coeff * * 0.2381 3.405
timestep ${dt}
thermo $d
# equilibration and thermalization
velocity all create ${Tinit} 102486 mom yes rot yes dist gaussian
fix NVT all nvt temp ${Tinit} ${Tinit} 10 drag 0.2
run 8000
# viscosity calculation, switch to NVE if desired
velocity all create $T 102486 mom yes rot yes dist gaussian
fix NVT all nvt temp $T $T 10 drag 0.2
#unfix NVT
#fix NVE all nve
reset_timestep 0
variable pxy equal pxy
variable pxz equal pxz
variable pyz equal pyz
fix SS all ave/correlate $s $p $d &
v_pxy v_pxz v_pyz type auto file S0St.dat ave running
variable scale equal ${convert}/(${kB}*$T)*$V*$s*${dt}
variable v11 equal trap(f_SS[3])*${scale}
variable v22 equal trap(f_SS[4])*${scale}
variable v33 equal trap(f_SS[5])*${scale}
thermo_style custom step temp press v_pxy v_pxz v_pyz v_v11 v_v22 v_v33
run 100000
variable v equal (v_v11+v_v22+v_v33)/3.0
variable ndens equal count(all)/vol
print "average viscosity: $v [Pa.s] @ $T K, ${ndens} atoms/A^3"
Lattice spacing in x,y,z = 5.376 5.376 5.376
Created orthogonal box = (0 0 0) to (21.504 21.504 21.504)
1 by 1 by 1 MPI processor grid
Created 256 atoms
using lattice units in orthogonal box = (0 0 0) to (21.504 21.504 21.504)
create_atoms CPU = 0.000 seconds
Generated 0 of 0 mixed pair_coeff terms from geometric mixing rule
Neighbor list info ...
update: every = 1 steps, delay = 0 steps, check = yes
max neighbors/atom: 2000, page size: 100000
master list distance cutoff = 15
ghost atom cutoff = 15
binsize = 7.5, bins = 3 3 3
1 neighbor lists, perpetual/occasional/extra = 1 0 0
(1) pair lj/cut, perpetual
attributes: half, newton on
pair build: half/bin/atomonly/newton
stencil: half/bin/3d
bin: standard
Setting up Verlet run ...
Unit style : real
Current step : 0
Time step : 4
Per MPI rank memory allocation (min/avg/max) = 3.219 | 3.219 | 3.219 Mbytes
Step Temp E_pair E_mol TotEng Press
0 250 -505.75228 0 -315.72564 -660.93588
2000 260.9494 -304.49791 0 -106.14856 6727.1349
4000 268.28925 -280.9705 0 -77.042081 7576.398
6000 247.08255 -291.05749 0 -103.24842 7119.7814
8000 243.68037 -289.28797 0 -104.06492 7219.3327
Loop time of 2.517 on 1 procs for 8000 steps with 256 atoms
Performance: 1098.451 ns/day, 0.022 hours/ns, 3178.388 timesteps/s, 813.667 katom-step/s
99.7% CPU use with 1 MPI tasks x 1 OpenMP threads
MPI task timing breakdown:
Section | min time | avg time | max time |%varavg| %total
---------------------------------------------------------------
Pair | 2.2503 | 2.2503 | 2.2503 | 0.0 | 89.40
Neigh | 0.18036 | 0.18036 | 0.18036 | 0.0 | 7.17
Comm | 0.055474 | 0.055474 | 0.055474 | 0.0 | 2.20
Output | 0.0002151 | 0.0002151 | 0.0002151 | 0.0 | 0.01
Modify | 0.019191 | 0.019191 | 0.019191 | 0.0 | 0.76
Other | | 0.01145 | | | 0.45
Nlocal: 256 ave 256 max 256 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Nghost: 3276 ave 3276 max 3276 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Neighs: 46355 ave 46355 max 46355 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Total # of neighbors = 46355
Ave neighs/atom = 181.07422
Neighbor list builds = 244
Dangerous builds = 0
Generated 0 of 0 mixed pair_coeff terms from geometric mixing rule
Setting up Verlet run ...
Unit style : real
Current step : 0
Time step : 4
Per MPI rank memory allocation (min/avg/max) = 3.223 | 3.223 | 3.223 Mbytes
Step Temp Press v_pxy v_pxz v_pyz v_v11 v_v22 v_v33
0 200 7066.7041 319.60155 6.2506333 56.723174 3.7765481e-05 1.4445258e-08 1.1895928e-06
2000 196.98509 5902.9807 321.93527 -175.50508 -16.929677 0.0018691456 5.3718108e-05 0.0002180816
4000 194.52952 5541.9832 96.040777 775.5341 181.33901 0.00022436972 0.00017742085 0.00031922146
6000 204.92295 6165.7212 297.68908 -161.36833 -15.416206 0.00013083564 0.00063286784 0.00026244527
8000 199.32515 6087.4832 -272.24938 -157.4138 -199.94347 4.7737412e-05 0.00068386149 0.0002487648
10000 195.7603 6177.1396 397.76544 92.607734 -619.4326 9.7729401e-05 0.0013421099 0.00084661253
12000 212.57747 5493.0044 -171.37027 -449.44221 -239.08507 7.400902e-05 0.0013048505 0.0013406102
14000 202.40279 5874.9961 201.72805 15.541866 -397.62761 0.00061732607 0.0011547585 0.0013120266
16000 209.90909 6199.5585 -50.498862 -41.95207 360.05886 0.00053724859 0.0010411796 0.0011712216
18000 196.97381 5955.6253 -26.300109 206.66948 32.226192 0.00046274052 0.00096287849 0.00094102404
20000 201.01783 5989.9773 -329.59192 -5.8825162 -480.12884 0.00047849469 0.00092755394 0.00084456549
22000 208.72749 5981.9669 325.01468 -3.1026811 -798.99079 0.00053217922 0.00083506521 0.00080100115
24000 199.88564 5627.6304 81.367123 -197.80008 54.829733 0.00052621194 0.00080635783 0.00070118945
26000 203.63895 6209.8358 -512.1482 -46.836387 29.96927 0.00048038283 0.00075832153 0.00066745301
28000 191.99506 5401.2449 -101.89095 -153.3097 248.52278 0.00045368162 0.00064592905 0.0006032091
30000 208.09257 6274.8131 -38.257924 23.465768 597.98381 0.00052979533 0.00060263807 0.00069813332
32000 204.83319 6081.6717 -181.14528 231.72795 203.01671 0.00071954055 0.00056401704 0.00064331406
34000 196.64115 5972.9357 190.19038 89.051849 286.76361 0.00070748417 0.0005185493 0.00062596249
36000 194.24625 5993.8049 761.44485 194.98796 -117.4918 0.00065126752 0.00055776907 0.00074698203
38000 199.27978 5658.5591 -306.04222 88.445545 -244.41237 0.00062067329 0.00056696842 0.00072112818
40000 205.52758 5662.5246 -5.5104539 -50.666093 120.27605 0.00059474146 0.00053386168 0.00067593238
42000 218.01758 6083.1113 -85.109792 -343.37344 307.55517 0.00058341511 0.00059429077 0.00064310369
44000 188.1028 5758.0974 -4.1313545 49.051024 40.712771 0.00056488264 0.00051529723 0.00064258864
46000 199.3865 5559.1248 13.80344 -196.4012 -143.89375 0.00059513021 0.00053033121 0.00060099484
48000 204.67468 6322.2413 -673.53469 -342.19106 -302.28136 0.00058265652 0.00052365417 0.00058211091
50000 199.22296 6099.5222 344.47482 158.92151 270.8337 0.00055861852 0.00052836712 0.00064108134
52000 187.19428 5798.4813 329.5885 -122.51274 487.73552 0.00053716045 0.00050506785 0.0006184784
54000 197.12012 6060.375 -415.06373 256.65941 232.56322 0.00062423414 0.00052867035 0.00060865003
56000 197.13363 5581.884 -413.22181 89.073966 151.3985 0.00060451273 0.00049883584 0.00062370265
58000 187.81162 5920.5033 440.15015 131.82012 -196.90585 0.00059578798 0.00049979739 0.00060304251
60000 197.70977 6006.9152 153.95076 -262.37065 -110.46897 0.00057048546 0.00050043449 0.00057484896
62000 218.73134 6178.118 -285.69348 216.17161 -2.0630058 0.00055018898 0.00047222346 0.00060468
64000 205.3228 6353.7275 20.065104 481.64723 156.80247 0.00052046678 0.00045283408 0.00058842057
66000 212.20017 5942.5776 -9.5024906 9.3199323 154.58966 0.0005040516 0.00045958409 0.00056742747
68000 204.35542 5961.9852 28.233115 -13.708293 -408.2356 0.00046586692 0.00043708538 0.00054860558
70000 206.4871 5189.6468 -180.40878 319.27257 -332.88389 0.00049520066 0.00042367165 0.00055127412
72000 206.50001 5281.6869 -453.16961 -242.27304 66.597658 0.00049076354 0.00040197711 0.00059077627
74000 212.66631 6641.9682 148.0256 -79.67418 291.93891 0.00052382486 0.00042006659 0.00058019466
76000 179.47415 5893.4833 -317.02424 577.0005 -237.73572 0.00052672716 0.00040112908 0.00055664684
78000 185.548 6155.9532 -20.396775 -217.59395 89.859402 0.00052564448 0.00040873133 0.00054650555
80000 208.32885 5915.2026 49.423178 408.43617 83.79932 0.00055143634 0.00038067513 0.00057996172
82000 196.45979 5938.8173 62.826363 -611.54378 -287.13073 0.0005106022 0.00038549757 0.00058566144
84000 206.87171 5905.7231 97.488717 -567.61326 -63.026599 0.00050876699 0.00036730565 0.00057860502
86000 210.50301 6013.177 -194.06503 -105.16641 57.23711 0.00053703746 0.00038625663 0.00057714933
88000 202.97118 6035.7137 -62.383506 360.78618 298.57751 0.000501343 0.00040719383 0.00055623793
90000 202.80417 5609.4755 -136.35588 -57.792138 -0.14283701 0.00052381869 0.00040099966 0.00054034592
92000 212.79394 5747.1979 -182.96364 -61.031676 338.53143 0.00051298745 0.00040760181 0.00052777593
94000 205.82181 5388.1114 33.354151 196.97247 2.1924511 0.00053429763 0.00040501577 0.00051622245
96000 195.95454 6053.8332 180.54921 209.79834 -715.20699 0.00051458668 0.00041586956 0.00052313913
98000 190.92072 5689.6723 -551.51097 60.226037 199.69565 0.00050715047 0.00043312192 0.00049829024
100000 199.41605 5884.9881 -342.86069 184.58956 231.23881 0.00050743068 0.00041900794 0.00053758923
Loop time of 31.8665 on 1 procs for 100000 steps with 256 atoms
Performance: 1084.526 ns/day, 0.022 hours/ns, 3138.095 timesteps/s, 803.352 katom-step/s
100.1% CPU use with 1 MPI tasks x 1 OpenMP threads
MPI task timing breakdown:
Section | min time | avg time | max time |%varavg| %total
---------------------------------------------------------------
Pair | 28.562 | 28.562 | 28.562 | 0.0 | 89.63
Neigh | 2.0367 | 2.0367 | 2.0367 | 0.0 | 6.39
Comm | 0.70197 | 0.70197 | 0.70197 | 0.0 | 2.20
Output | 0.0026552 | 0.0026552 | 0.0026552 | 0.0 | 0.01
Modify | 0.41521 | 0.41521 | 0.41521 | 0.0 | 1.30
Other | | 0.1481 | | | 0.46
Nlocal: 256 ave 256 max 256 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Nghost: 3258 ave 3258 max 3258 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Neighs: 46261 ave 46261 max 46261 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Total # of neighbors = 46261
Ave neighs/atom = 180.70703
Neighbor list builds = 2718
Dangerous builds = 0
average viscosity: 0.000488009286555395 [Pa.s] @ 200 K, 0.0257443666020476 atoms/A^3
'\n# Sample LAMMPS input script for viscosity of liquid Ar\n\nunits real\nvariable T equal 200.0 # run temperature\nvariable Tinit equal 250.0 # equilibration temperature\nvariable V equal vol\nvariable dt equal 4.0\nvariable p equal 400 # correlation length\nvariable s equal 5 # sample interval\nvariable d equal $p*$s # dump interval\n\n# convert from LAMMPS real units to SI\n\nvariable kB equal 1.3806504e-23 # [J/K] Boltzmann\nvariable atm2Pa equal 101325.0\nvariable A2m equal 1.0e-10\nvariable fs2s equal 1.0e-15\nvariable convert equal ${atm2Pa}*${atm2Pa}*${fs2s}*${A2m}*${A2m}*${A2m}\n\n# setup problem\n\ndimension 3\nboundary p p p\nlattice fcc 5.376 orient x 1 0 0 orient y 0 1 0 orient z 0 0 1\nregion box block 0 4 0 4 0 4\ncreate_box 1 box\ncreate_atoms 1 box\nmass 1 39.948\npair_style lj/cut 13.0\npair_coeff * * 0.2381 3.405\ntimestep ${dt}\nthermo $d\n\n# equilibration and thermalization\n\nvelocity all create ${Tinit} 102486 mom yes rot yes dist gaussian\nfix NVT all nvt temp ${Tinit} ${Tinit} 10 drag 0.2\nrun 8000\n\n# viscosity calculation, switch to NVE if desired\n\nvelocity all create $T 102486 mom yes rot yes dist gaussian\nfix NVT all nvt temp $T $T 10 drag 0.2\n#unfix NVT\n#fix NVE all nve\n\nreset_timestep 0\nvariable pxy equal pxy\nvariable pxz equal pxz\nvariable pyz equal pyz\nfix SS all ave/correlate $s $p $d &\n v_pxy v_pxz v_pyz type auto file S0St.dat ave running\nvariable scale equal ${convert}/(${kB}*$T)*$V*$s*${dt}\nvariable v11 equal trap(f_SS[3])*${scale}\nvariable v22 equal trap(f_SS[4])*${scale}\nvariable v33 equal trap(f_SS[5])*${scale}\nthermo_style custom step temp press v_pxy v_pxz v_pyz v_v11 v_v22 v_v33\nrun 100000\nvariable v equal (v_v11+v_v22+v_v33)/3.0\nvariable ndens equal count(all)/vol\nprint "average viscosity: $v [Pa.s] @ $T K, ${ndens} atoms/A^3"\n'